残念ながら当らなかった人は、運が悪かったのでしょうか?ここでラッフルに当たる確率を計算してみましょう!!(>▽<)
問題
ラッフルチケットは全部で1062枚売れました。景品は17個(重複を含む)あります。買ったチケットが4枚だとすると、景品が少なくとも1つ当たる確率は何%でしょう?(有効数字は2桁とします。)
解答
6.3%、つまり16分の1くらいです。
解説
この手の問題は、1つも当たらない確率をまず計算して、100%から引くと攻めやすいです。
1つも当たらない確率は17個の景品がそれぞれが当たらない確率をかけた(×)ものになります。
1個目は全体(1062枚)の中から外れチケット(1058枚)を選びますから、1058÷1062です。
2個目は残り(1061枚)の中から外れチケット(1057枚)を選びますから、1057÷1061です。
3個目は残り(1060枚)の中から外れチケット(1056枚)を選びますから、1056÷1060です。
4個目は残り(1059枚)の中から外れチケット(1055枚)を選びますから、1055÷1059です。
5個目は残り(1058枚)の中から外れチケット(1054枚)を選びますから、1054÷1058です。
6個目は残り(1057枚)の中から外れチケット(1053枚)を選びますから、1053÷1057です。
7個目は残り(1056枚)の中から外れチケット(1052枚)を選びますから、1052÷1056です。
8個目は残り(1055枚)の中から外れチケット(1051枚)を選びますから、1051÷1055です。
9個目は残り(1054枚)の中から外れチケット(1050枚)を選びますから、1050÷1054です。
10個目は残り(1053枚)の中から外れチケット(1049枚)を選びますから、1049÷1053です。
11個目は残り(1052枚)の中から外れチケット(1048枚)を選びますから、1048÷1052です。
12個目は残り(1051枚)の中から外れチケット(1047枚)を選びますから、1047÷1051です。
13個目は残り(1050枚)の中から外れチケット(1046枚)を選びますから、1046÷1050です。
14個目は残り(1049枚)の中から外れチケット(1045枚)を選びますから、1045÷1049です。
15個目は残り(1048枚)の中から外れチケット(1044枚)を選びますから、1044÷1048です。
16個目は残り(1047枚)の中から外れチケット(1043枚)を選びますから、1043÷1047です。
17個目は残り(1046枚)の中から外れチケット(1042枚)を選びますから、1042÷1046です。
気づきましたでしょうか?5個目から13個目は分子と分母が他の確率と打ち消しあうのです。
つまり、確率は以下の式に簡略化されます。
(1045×1044×1043×1042)÷(1062×1061×1060×1059)
=0.9374、、、
これがすべてハズれる確率です。
つまりどれか1個でも当たる確率は
1-0.9375=0.06259、、、
有効数字2桁なので、確率は0.063、つまり6.3%です。
一般化
買ったチケットの枚数がn枚だった時、どれか1つ当たる確率は
1-((1042)×(1042+1)、、、×(1042+n-1))÷((1062)×(1062-1)、、、×(1062-n+1))
です。
さらに一般化
売れたチケットの枚数がs枚、景品がp個、買ったチケットの枚数がn枚だった時、どれか1つ当たる確率は
1-((s-p-n+1)×(s-p-n+2)、、、×(s-p))÷((s)×(s-1)、、、×(s-n+1))
となります。
こうとも書けます。
1-((s-n)!÷(s-p-n)!)÷(s!÷(s-p)!)
=1-((s-n)!×(s-p)!)÷(s!×(s-p-n)!)
n「!」とは階乗のことで、1からnまでの数をかけた結果です。英語では「factorial」と呼びます。
順列と組み合わせを使うともっと簡単に割り出せます。
分子は外れ券の中から景品数分を選ぶ組み合わせ。分母は全体から景品数分を選ぶ組み合わせ。組み合わせの公式に割り当てると、上と同じ結果になりますね。
組み合わせの公式
順列は英語で「permutation」、組み合わせは「combination」です。
おしゃれな記号を使うとこうです。
「Π(パイ)」は下の数から上の数までを式に入れて、かけあわせた結果です。掛け算の結果(積)は英語で「product」。頭文字の「P」はギリシャ文字で「パイ」なのでこうなっているのだと思います。ちなみに円周率の「π」は同じ文字の小文字です。
まとめ
4枚は全体の0.4%にもならないのに何かが当たる確率が6.3%ってちょっとお得な気分ですね。(>▽<)-3
ちなみに、確率を50%以上にしたかったら43枚買う必要がありました!!たった4%の投資で、豪華賞品をもらえる確率が半々!!(>▽<)ノ
何のまとめだかわかりませんね、、、( ゜Д゜)

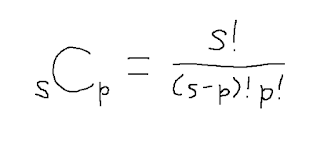

0 件のコメント:
コメントを投稿